探索Abelian「難度平滑演算法」（DSA）

介紹

從第 284,000 區塊起，Abelian 區塊鏈調整了難度機制；下方圖表顯示此變動對區塊難度與平均出塊時間的影響。

‍

本文將簡要說明新的難度平滑調整機制運作原理，並示範如何計算礦機新的目標值與位元參數。

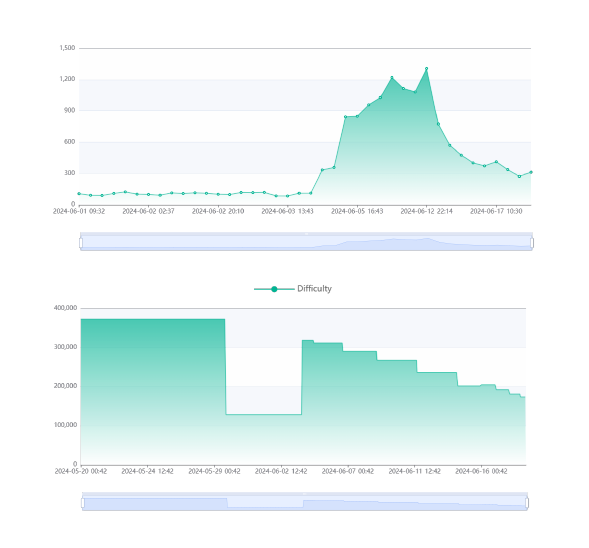
難度平滑調整（DSA）

工作量、哈希率和目標

在挖礦過程中，礦工會先計算區塊頭的雜湊值，並檢驗該值是否低於區塊設定的目標值。

由於使用的哈希演算法是 SHA-256，因此存在 2²⁵⁶ 個可能的哈希率值，礦工成功挖到目標哈希率值的區塊。這意味著成功挖到區塊的機率為

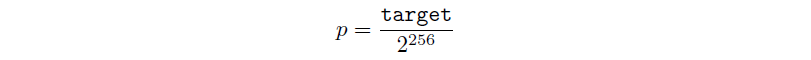
因此，礦工成功所需的預期嘗試次數為

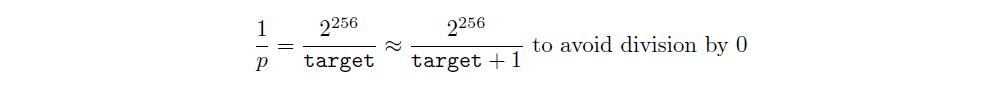
我們將單區塊的工作量定義為預期嘗試次數，並以每秒完成的嘗試次數表示為雜湊率。

注意：Explorer 的 API 僅公開位元值（bits），不直接顯示目標值。例如，https://api.abelian.info/v1/block/284800 會顯示位元資訊而非目標值。

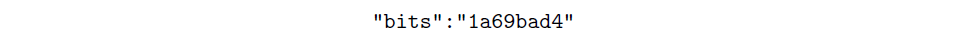
該位元（bits）以緊湊格式表示目標值，我們可將其還原為完整目標值，方法如下：

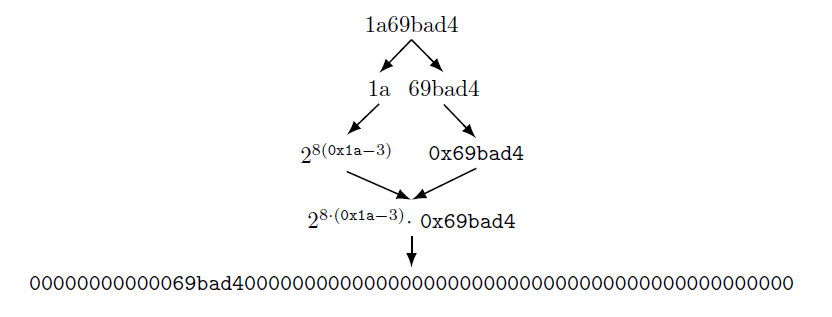
DSA 摘要

註：一個時隙由 200 個連續區塊組成，例如區塊 284800–284999 為同一時隙。

‍

新的難度平滑演算法已於區塊高度 284000 啟用，取代舊有調整機制。該演算法會為每個區塊重算目標難度：先計算過去 20 個區塊的加權平均雜湊率，然後根據此加權平均值設定新的目標難度，使在下一區塊的雜湊率等於預測加權平均時，平均出塊時間約為 256 秒。

‍

首先，給定目標區塊數與區塊槽時間（即該時隙中首末區塊挖出之間的秒數），我們可將該時隙的雜湊率計算如下：

或者等價地說，

在計算完過去 20 個時隙的哈希率（哈希率ᵢ₋₂₀、哈希率ᵢ₋₁₉、…、哈希率ᵢ₋₁）後，我們接著求其加權平均哈希率：

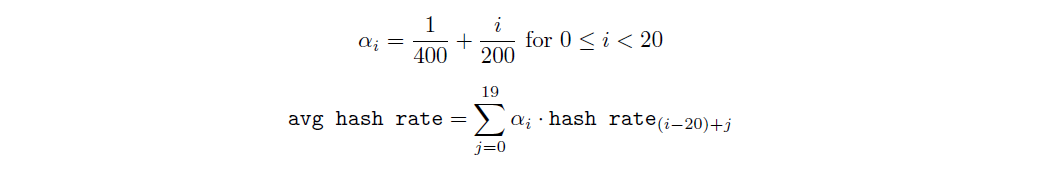
接著比較加權平均哈希率與最近一個時隙的哈希率（哈希率ᵢ₋₁）之比；若該比值小於 1/4 或大於 4，則將其截斷到 [1/4, 4] 範圍內。

‍

註：假定下一個時隙的哈希率等於最近一個時隙的哈希率，若新難度計算會使平均出塊時間超過 4 × 256 = 1024 秒或低於 256 ÷ 4 = 64 秒，則會將平均出塊時間限制在 64 到 1024 秒之間。

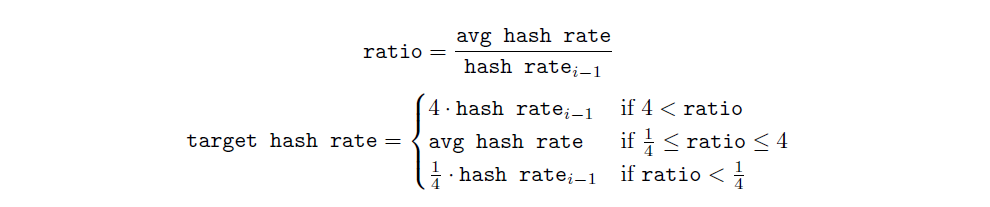
最後，我們以預期下一個時隙的哈希率將達到目標哈希率為前提，據此計算新的目標值。基於哈希率與目標值的關係：

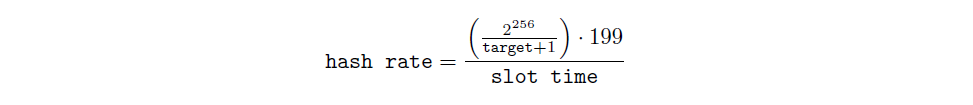
我們希望下一時段的總時長為 199 個區塊 × 256 秒／區塊，因此新的目標時長為：

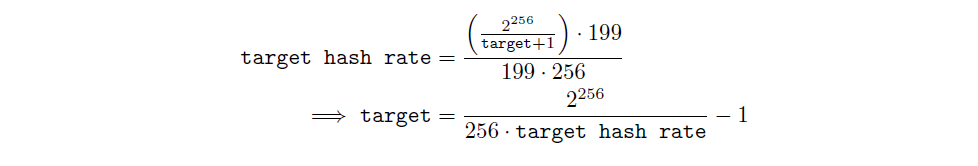
最後，我們把目標值轉為位元（bits）的緊湊表示，並在後續所有計算與比較中使用該位元值。

‍

範例

我們以計算時隙 284800–284999 的目標值作為示範，說明難度平滑調整（DSA）的運作。

首先，我們從 Explorer 的 API 獲取前 20 個插槽的參數，並用它們來計算每個插槽的哈希率。例如，我們看到槽位 280800–280999 具有以下參數：

我們將比特轉換為目標：

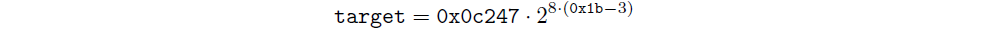
我們計算時段時間：

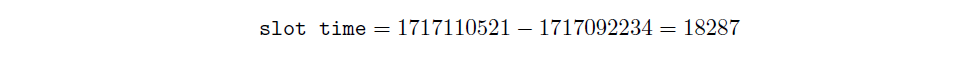
一旦確定了目標時間和時隙時間，我們就計算哈希率：

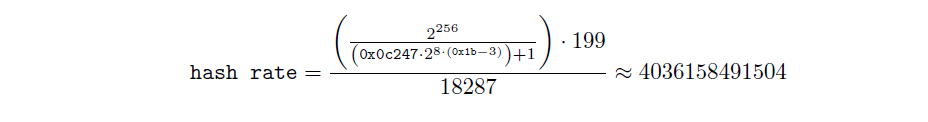
我們對過去 20 個位置重複這些步驟：

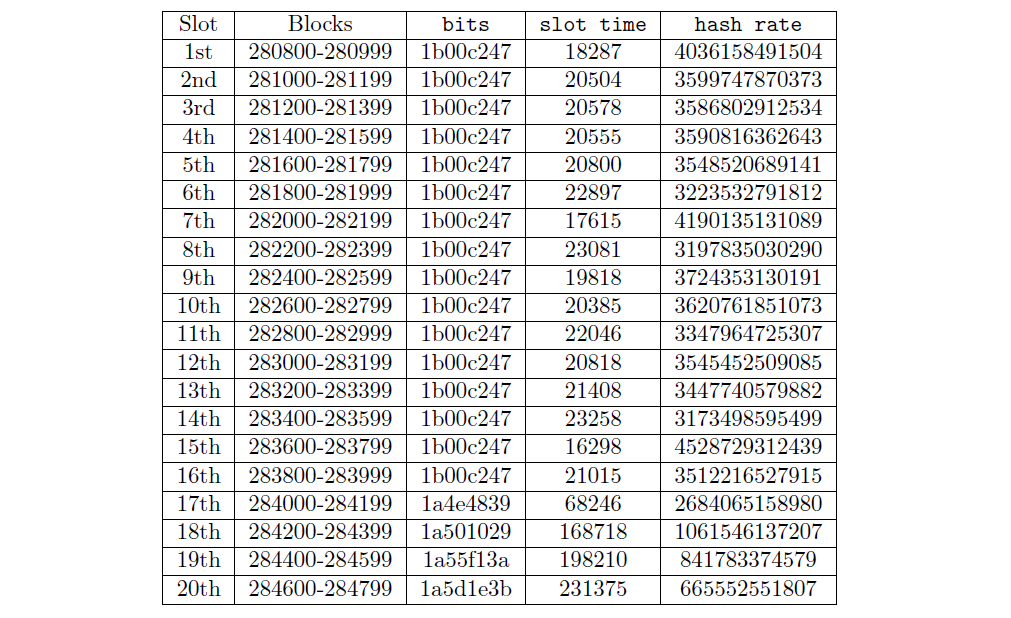
一旦我們獲得了過去 20 個插槽的哈希率，我們就計算加權平均哈希率：

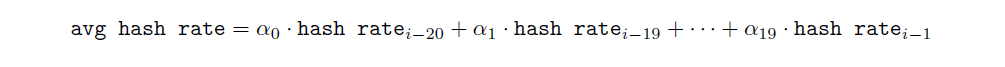
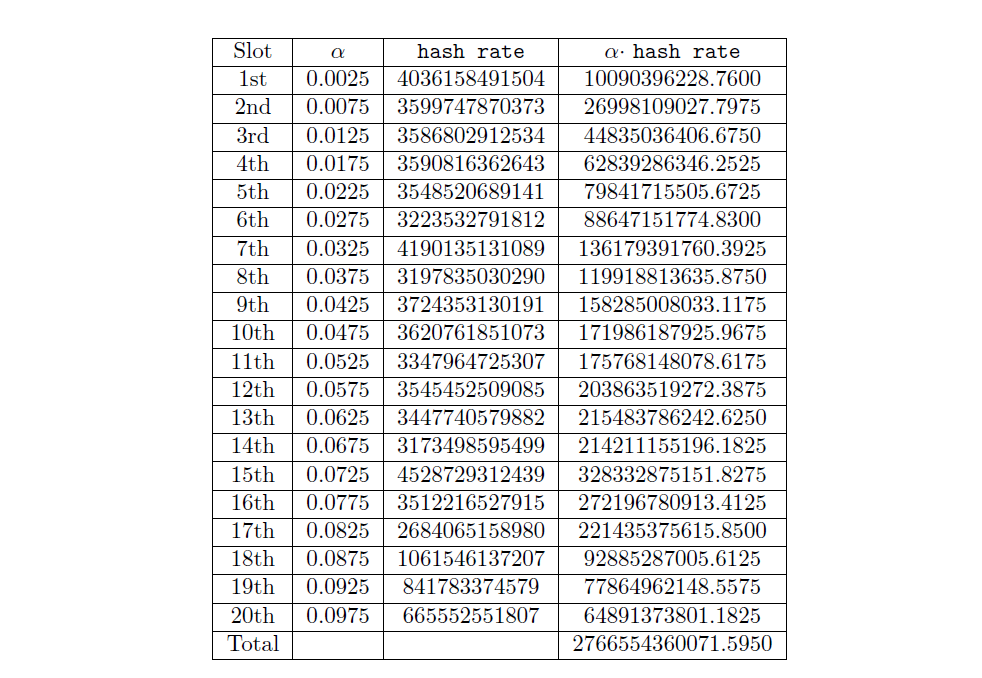
然後我們計算該比率：

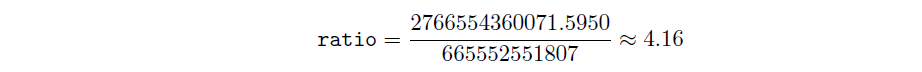
由於比率 = 4.16 > 4，我們將目標哈希率限制在 4 · 哈希率ᵢ₋₁) = 2662210207228。

‍

最後，我們可以使用目標哈希率來計算新的目標：

現在我們有了目標值，我們可以透過重複將尾數除以 256，並將指數從 3 開始加 1 來找到該位的值，直到尾數 < 0x00800000。

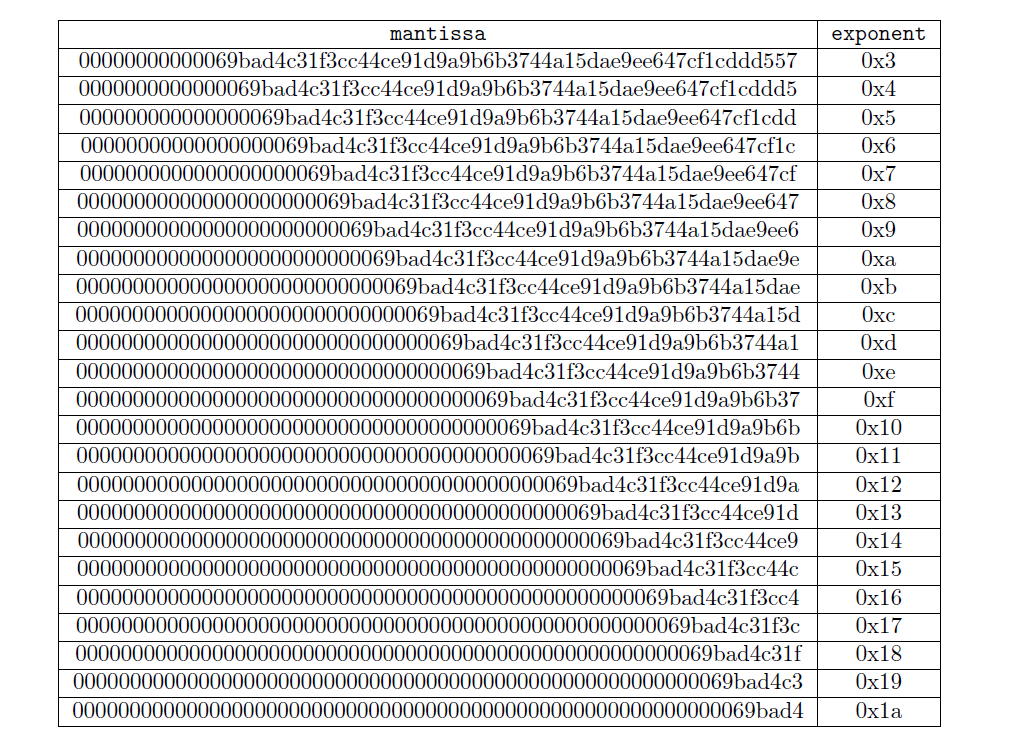
我們發現該位的值為 1a69bad4，我們將在後續計算中使用該位對應的目標值：

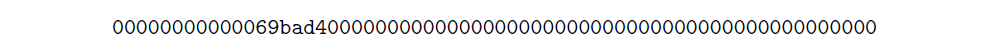
我注意－我們也可以透過瀏覽器 API 找到難度值，如下所示：

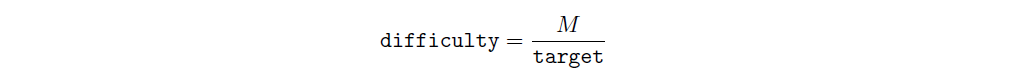
其中 M 是最大可能的難度（其位元數為 1d017c38）。

例如，對於插槽 284800–284999，

延伸閱讀

要了解 DSA 的優勢，請進一步了解演算法如何快速適應算力波動並穩定平均出塊時間。

Advantages of Abelian’s Difficulty Smoothing Algorithm (DSA)

‍