
Introduction
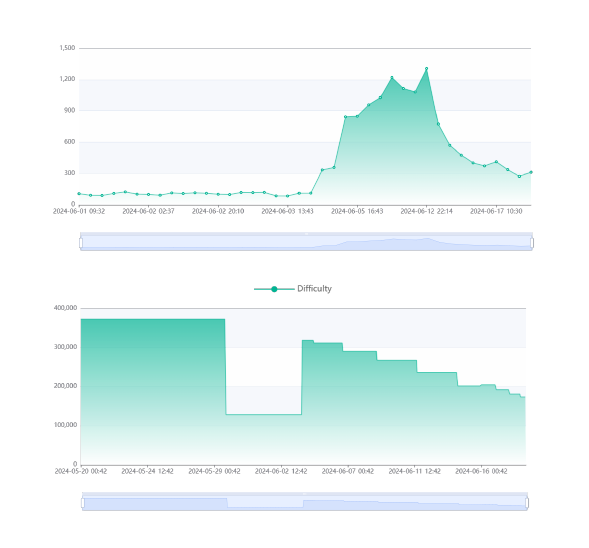
The Abelian blockchain has undergone a change in its difficulty adjustment scheme starting block 284000, and its effects on the block difficulty and average block time can be seen in the graphs below.
This writeup will briefly explain how the new adjustment mechanism (Difficulty Smoothing Adjustment) works, and follow it up with an example of calculating a slot’s new target and bits parameters.
Difficulty Smoothing Adjustment (DSA)
Work, Hash Rate, & Target
When mining a block, a miner would first compute the hash value of its header, and then check if it’s less than the block’s target.

Since the hash algorithm used is SHA-256, there are 2²⁵⁶ possible hash rate values, and the miner succeeds in mining a block for target possible values. This means the probability of successfully mining a block would be
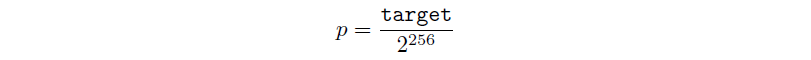
and therefore the expected number of attempts until a miner succeeds would be
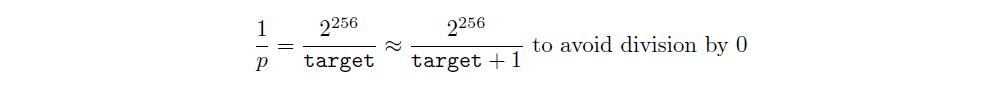
We define work (for a single block) to be this number of expected attempts, and we define the hash rate as the amount of work done per second.

Note: Instead of target, we only see the bits value in the Explorer’s API. For example, https://api.abelian.info/v1/block/284800 displays
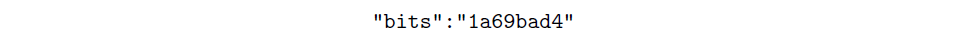
The bits value represents the target value in compact form, which we can convert back to its full form like so:
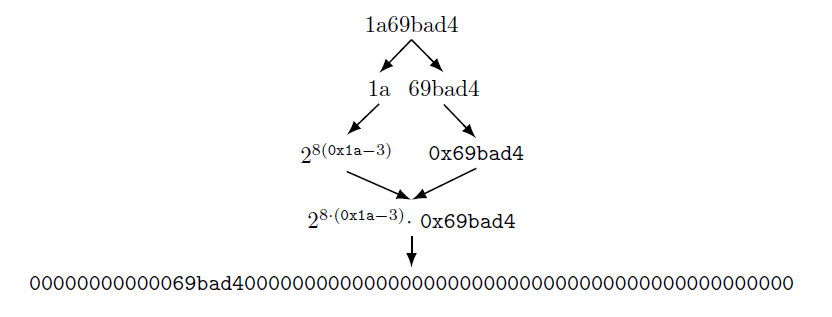
DSA Summary
Note: A slot consists of 200 consecutive blocks. For example, 284800–284999 is a single slot.
The new Difficulty Smoothing Algorithm was launched at block 284000, replacing the original adjustment mechanism. It now recalculates the target for each slot, by first calculating a weighted average hash rate over the past 20 slots, then using the weighted hash rate to come up with a new targetso that the average time taken for a block to be mined would be 256 seconds, assuming the next slot’s hash rate matches the predicted weighted hash rate.
First, given a target and slot time (number of seconds between the mining time of the first and last block in the slot), we can calculate a slot’s hash rate like so:

Or equivalently,

Once we calculate the hash rate of the past 20 slots (hash rateᵢ₋₂₀, hash rateᵢ₋₁₉, . . . , hash rateᵢ₋₁), we then proceed with calculating the weighted average hash rate:
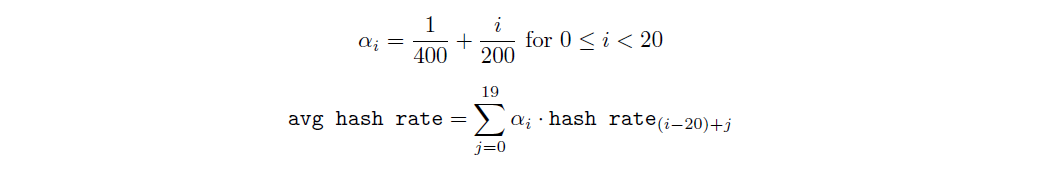
We then compare the ratio between avg hash rate and the most recent slot’s hash rate (hash rateᵢ₋₁). If the ratio is below 1/4 or above 4, we clamp it between these values.
Note: Assuming the hash rate of the next slot doesn’t change from the most recent slot, and if the newly-calculated difficulty would increase the average block time to over 4 · 256 = 1024 seconds, or decrease it to below 256/4 = 64 seconds, this would clamp the average block time between these values.
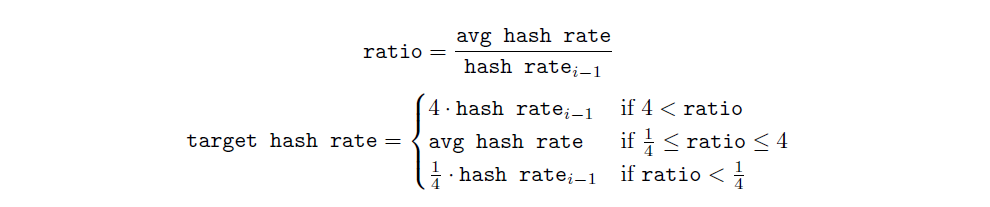
Finally, we ‘predict’ the next slot’s hash rate would be target hash rate, and we would calculate the new targetvalue accordingly. Given the relationship between hash rate and target:
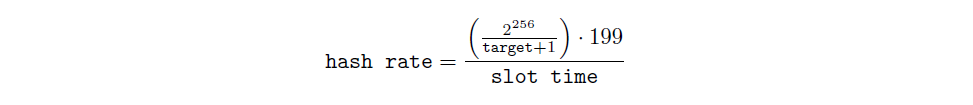
We wish for the upcoming slot timeto be 199 · 256 seconds, therefore our new target would be:
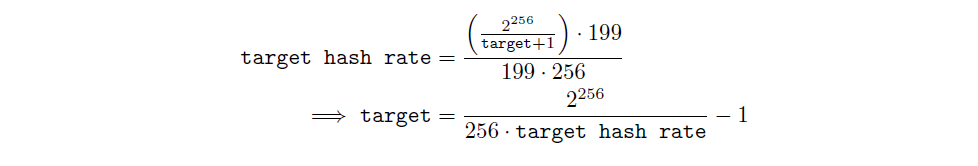
And finally, we would convert our target into compact form as bits, and use bits’s value in all future calculations and comparisons.
Illustrative Example
We demonstrate DSA by calculating the target for the slot 284800–284999.
First, we retrieve the parameters of the previous 20 slots from the Explorer’s API, and use them to calculate each slot’s hash rate. For example, we see that slot 280800–280999 has the following parameters:

We convert bits into target:
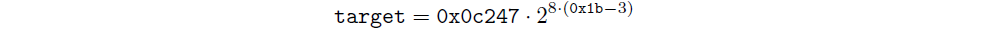
And we calculate slot time:
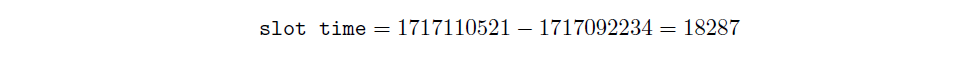
Once we have targetand slot time, we calculate hash rate:
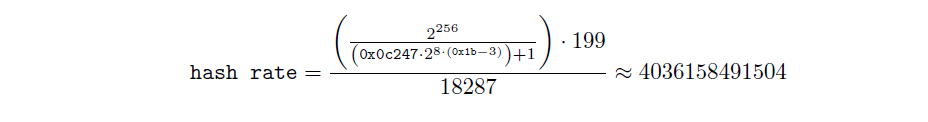
We repeat these steps for each of the past 20 slots:
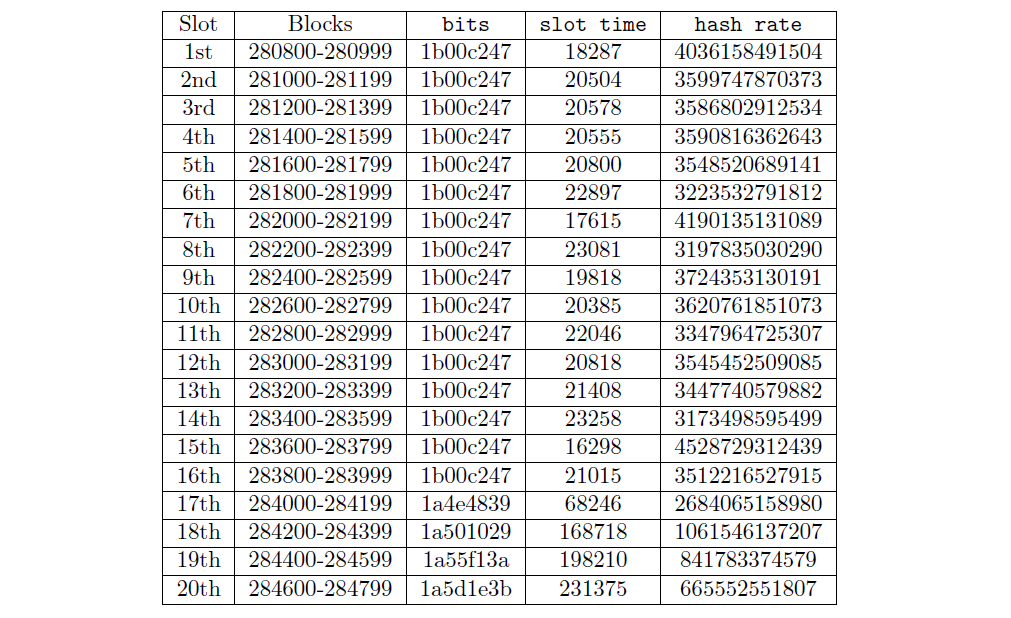
Once we have the past 20 slots’ hash rates, we calculate the weighted avg hash rate:
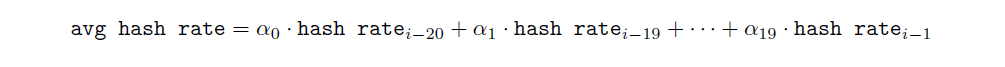
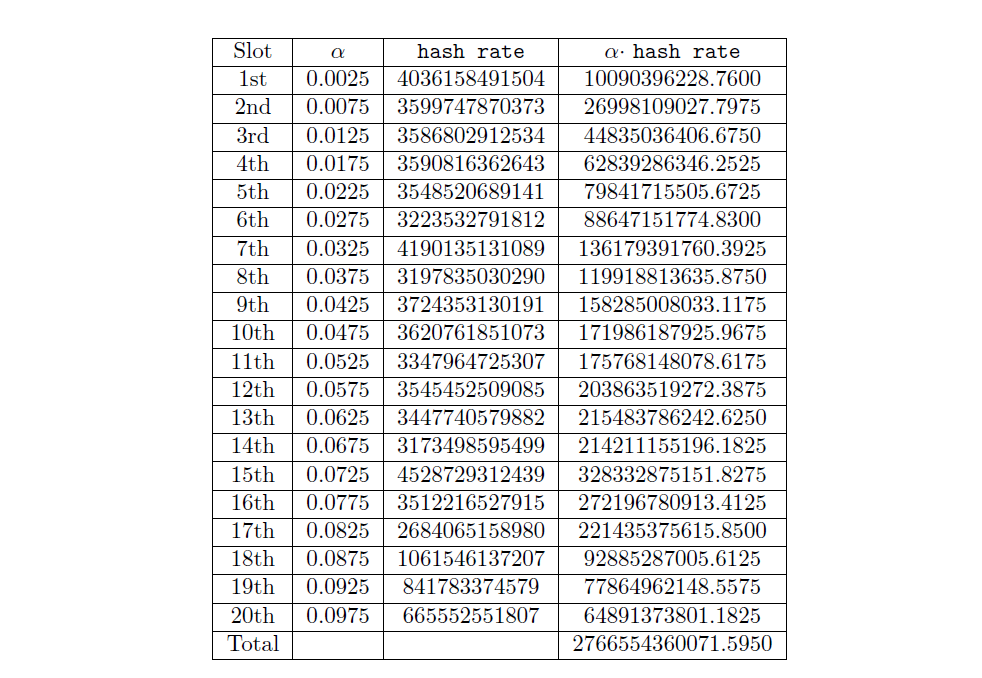
We then compute theratio:
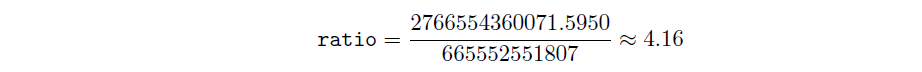
Since ratio = 4.16 > 4, we clamp target hash rate to 4 · hash rateᵢ₋₁) = 2662210207228.
Finally, we can use target hash rate to compute the new target:

Now that we have the target, we can find the bits value by repeatedly dividing the mantissa by 256 and incrementing the exponent by 1 starting from 3, until mantissa < 0x00800000.
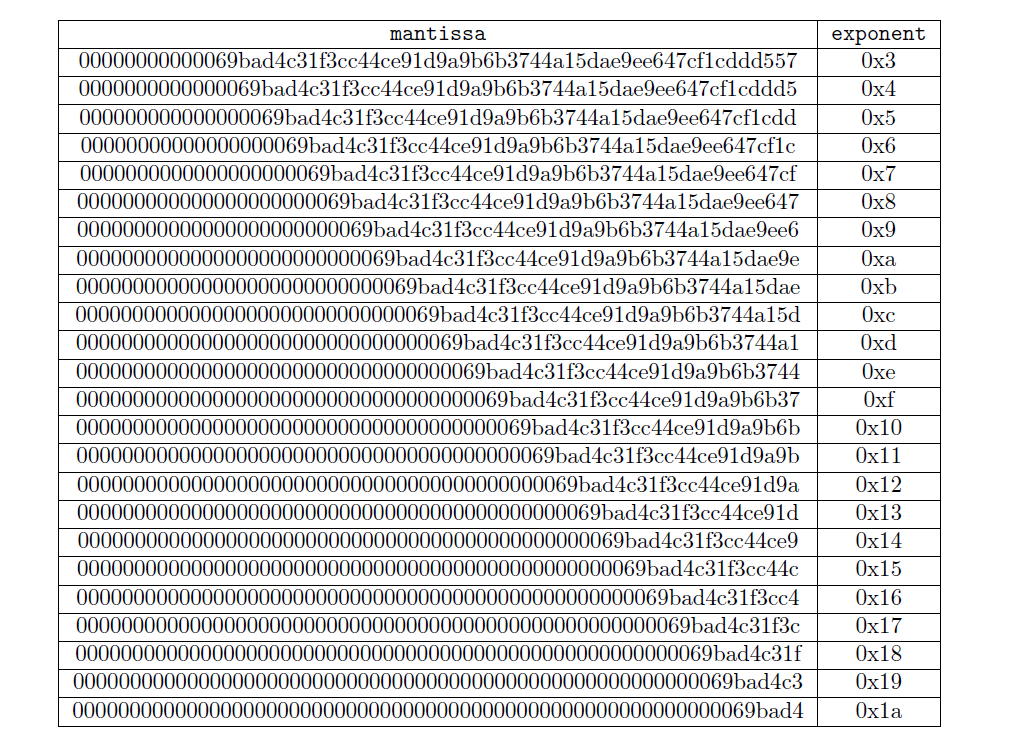
We find the bits value to be 1a69bad4, and we will use the bits’s corresponding targetvalue in future calculations:
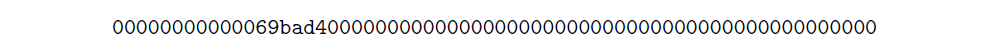
Note — we can also find the difficulty value as shown in the Explorer’s API like so:
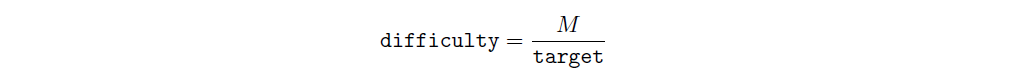
where M is the maximum possible difficulty (whose bits is 1d017c38).
For example, for slot 284800–284999,

Further reading
For more about the advantages of DSA, learn more about how the algorithm quickly adapts to hashrate fluctuations and stabilizes the average block time.
Advantages of Abelian’s Difficulty Smoothing Algorithm (DSA)

アーベルはポスト量子世界の基盤を構築しています
Abelian は、量子の脅威に耐えるように設計されたレイヤー 1 ブロックチェーンです。 NIST (国立標準技術研究所) は、耐量子暗号化とデジタル署名のための複数の格子ベースの暗号アルゴリズムをすでに承認しています。格子ベースの暗号化、多層プライバシー、堅牢な分散化により、Abelian はデジタル資産の安全性、プライベート性、将来性を確保します。


